Vietnamese Version

Around 2014 or 2015, many software engineers began to immerse themselves in a relatively new field: machine learning. For those loyal to Microsoft, the typical “hello world” program in this realm began with training a model using free data from the New York Cab dataset provided by Microsoft.

Some enthusiasts went further, downloading stock price data from Yahoo Finance to continue refining their models. But the honeymoon phase soon passed. Monotony crept in — mostly due to the limited depth and diversity of available data.

A spark of an idea arose in me: If we have artificial intelligence, why not artificial data? How do we create it? At that time, I was writing a simple “hello world” for polynomial regression, starting with a basic cubic function...

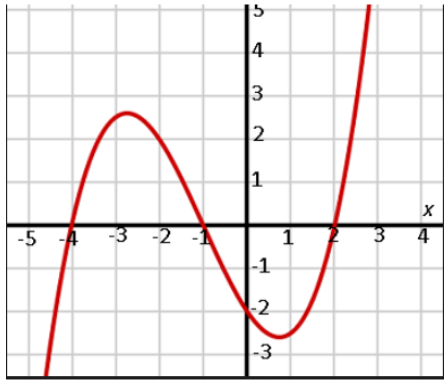
Suddenly, I realized: polynomials often carry religious undertones. There is a heaven, a hell, and in between, a brief stretch of life — where turbulence happens intensely and unpredictably. Like the graph of a cubic function: if each unit of x equals 10 years, then the range from x = -4 to x = 2 represents 60 years of life. In that span, we live — sometimes soaring, sometimes falling. But beyond that range, on both ends of the timeline, fluctuations subside. The graph trends linearly, steadily. It either rises eternally to heaven, or descends endlessly to hell.

The Calligraphy

Around this time, Châu Thụy introduced me to one of his calligraphy works, titled An (Peace). It remains my favorite among his creations.

Personally drawn to Buddhist philosophy, I interpreted this piece through that lens. Perhaps rightly, perhaps wrongly — my intent is merely to share, not to argue. I hope learned minds will kindly indulge this reflection.

The horizontal line represents the true mind — the source of true emotion, unconditioned and unwavering. For example, offering aid to a distant people — that act of compassion arises from the true mind. In contrast, loving someone because they are beautiful, and falling out of love when beauty fades, is a conditioned emotion — born from the deluded mind.

In the calligraphy, the wavy line represents the deluded mind. As these waves diminish, the deluded mind returns to the true mind. When illusion reunites with truth, peace emerges. All Dharma methods are paths to bring the deluded mind back to the true mind — the ten thousand Dharmas of the One Mind.

Somehow, this artwork, along with the Buddhist concept of impermanence (birth, existence, change, and extinction), and the endless cycle of samsara, deeply influenced the way I created my algorithm for artificial data generation.

The Pendulum Metaphor

Machine learning data must be complex and cyclical. Completely random phenomena cannot be learned from. And overly simple cycles are hardly worth learning.

I believe everything — every event, every creature, even us — is a pendulum, eternally swinging. Rising and falling, pausing and moving — birth, existence, change, extinction.

No pendulum swings in isolation. We interact with the world around us. We are influenced by others’ pendulums, and in turn, we influence them.

Imagine you are a pendulum oscillating left to right. Your lover is another pendulum swinging in and out, along a different axis, but at the same frequency. When your pendulum is at its highest point, theirs is at the lowest. The coordinated motion of these two pendulums forms a perfect, beloved circle.

But when your love becomes public — no longer hidden — external pendulums begin to influence your partner’s swings: supporters, jealous rivals, silent admirers. These new forces distort the once-perfect circle into unpredictable patterns. Some of these external pendulums even join your system and become part of your internal dynamics.

The Chain of Pendulums

With two pendulums, their operation can be visualized in animation. But with three or more, animations become too tangled to grasp. There is, however, a more abstract way.

Imagine each subsequent pendulum is anchored to the previous one, using the prior’s coordinates as its dynamic origin. This creates a chain of pendulums.

For example, with four pendulums: the first two form a large circle, the next two form smaller loops atop the large one.

Pendulums and Polar Coordinates

A sage sits still, a rock lies still — but this stillness is relative. Everything spins with the Earth’s rotation. With that in mind, I tied the origin of the pendulum chain to a rotating polar coordinate system. This gave birth to complex and beautiful motion cycles.

For instance, a single pendulum with a polar coordinate base spinning 3.3 times faster than the pendulum’s own frequency generates intricate loops. Rendered as a time series, these loops reveal a rich tapestry of data.

Theorem

Let f₁(t), f₂(t), ..., fₙ(t) be n periodic functions, each having a nonzero rational period T₁, T₂, ..., Tₙ, where Tᵢ ≠ 0 and Tᵢ ∈ ℚ. Then the sum:

F(t) = f₁(t) + f₂(t) + ... + fₙ(t)

is also a periodic function. That is, there exists a number T ≠ 0 such that:

F(t + T) = F(t), for all real values of t.

Step 1: Each component is periodic

For each i ∈ {1, ..., n}, we are given:

fᵢ(t + Tᵢ) = fᵢ(t)

Step 2: Determine a common period

Since all Tᵢ are nonzero rational numbers, there exists a number T that is a common multiple of all the Tᵢ.
For example, we may choose:

T = LCM(T₁, T₂, ..., Tₙ)

Then for every i:

fᵢ(t + T) = fᵢ(t)

Step 3: The sum is also periodic

Since all fᵢ repeat after T, the total sum satisfies:

    F(t + T) = f₁(t + T) + f₂(t + T) + ... + fₙ(t + T)
             = f₁(t) + f₂(t) + ... + fₙ(t) = F(t)
    

Note on the direction of time

If T is a period, then so is -T, since:

f(t + T) = f(t) ⇒ f(t - T) = f((t - T) + T) = f(t)

Therefore, periodic functions repeat in both directions of time: forward and backward.

Cultural Example: Heavenly Stems and Earthly Branches

In traditional East Asian calendars:

• The "Heavenly Stems" have a 10-year cycle: Giáp, Ất, Bính, Đinh, Mậu, Kỷ, Canh, Tân, Nhâm, Quý.
• The "Earthly Branches" have a 12-year cycle: Tý, Sửu, Dần, Mão, Thìn, Tỵ, Ngọ, Mùi, Thân, Dậu, Tuất, Hợi.

When paired to form designations like "Nhâm Dần" or "Quý Mão", the full cycle only repeats every 60 years, since LCM(10, 12) = 60.

This is a perfect real-world example of combining two periodic systems with different periods into one composite system with a larger common cycle.

Remarks

• The resulting period may be smaller than T if the functions cancel each other in structure.
• If any of the Tᵢ is irrational (e.g., √2 or π), the sum F(t) is no longer periodic — it becomes a quasi-periodic function.