English Version

Vào những năm 2014, 2015, nhiều kỹ sư lập trình (software engineers) bắt đầu dấn thân vào một lĩnh vực còn khá mới: tinh luyện máy (machine learning).
Nếu là tín đồ của Microsoft, hẳn ai cũng từng bắt đầu chương trình “hello world” về luyện máy, bằng cách sử dụng nguồn dữ liệu New York Cab miễn phí từ Microsoft để tinh luyện mô hình đầu tiên của mình. Đi xa hơn, có người tải xuống dữ liệu giá cổ phiếu từ Yahoo Finance để tiếp tục quá trình tinh luyện mô hình.
Nhưng rồi, giai đoạn trăng mật qua đi. Sự nhàm chán bắt đầu len lỏi — phần nhiều là do nguồn dữ liệu hạn hẹp, thiếu chiều sâu và tính đa dạng.

Một ý tưởng bắt đầu nhen nhóm trong tôi:
Nếu đã có trí tuệ nhân tạo, tại sao không có dữ liệu nhân tạo?
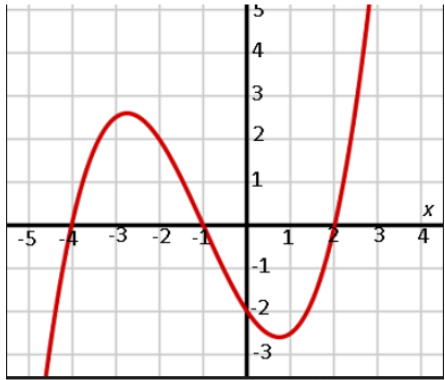
Làm thế nào để tạo ra nó? Trong khi tôi đang thử lập trình một phiên bản “hello world” cho phục chế đa thức (polynomial regression), khởi đầu với một hàm bậc ba đơn giản…

Tự nhiên tôi nhận ra: các đa thức thường mang sắc thái tôn giáo. Có thiên đàng, có địa ngục. Và ở giữa là một đoạn ngắn ngủi của đời sống — nơi sự thăng trầm diễn ra.
Như đồ thị của hàm bậc ba phía trên: nếu mỗi đơn vị của x là 10 năm, thì khoảng từ x=−4 đến x=2 chính là 60 năm cuộc đời. Trong khúc đó, ta sống — có lúc lên cao, có lúc rơi sâu. Nhưng rồi ra khỏi đoạn ấy, về hai đầu của trục thời gian, mọi biến động lặng xuống. Đồ thị thiên về đồng biến tuyến tính. Nó cứ thế trôi mãi về một hướng – hoặc vĩnh viễn đi lên thiên đàng, hoặc rơi xuống đáy địa ngục.

Giai đoạn này anh Châu Thuỵ có giới thiệu cho tôi một bức bút hoạ của anh mà đặt tên cho nó là An. Đây là bức tôi thích nhất trong các tác phẩm của anh.

Tôi nghĩ là bản thân mình thích quan niệm phật giáo. Thành ra tôi nhận xét bức bút hoạ này dưới sự chi phối của phật giáo quan. Có thể đúng có thể sai, ở đây tôi chỉ muốn chia sẻ chứ không phải tranh luận. Mong cao bậc trí giả đừng câu nệ.

Đường nằm ngang là chân tâm, chân tâm sanh chân tình, chân tình không bị điều kiện hoá nên không biến động. Ví dụ bạn đóng góp cứu trợ một dân tộc xa lạ. Đó là nghĩa cử, việc nghĩa xuất phát từ chân tâm. Trong khi đó có thể, bạn yêu thương một người tình vì người ấy đẹp, khi người đó không còn đẹp nữa tình cảm của bạn đổi thay. Đó là vọng tình bị điều kiện hoá. Vọng tình sinh ra từ vọng tâm. Trong bức bút hoạ, đường gợn sóng chính là vọng tâm. Khi đường vọng tình nhỏ đi tức vọng tâm đi lần về với chân tâm. Khi vọng về với chân thì an lành tự xuất hiện. Vạn pháp môn dùng để tu tập đưa vọng tâm về với chân tâm gọi là vạn pháp duy tâm nhất.

Không hiểu thế nào, mà hình ảnh bức An của anh Châu Thuỵ cùng khái niệm thăng trầm (sanh, trụ, dị, diệt) và sự luân hồi vô thuỷ vô chung ảnh hưởng đến việc tạo ra giải thuật tạo dữ liệu nhân tạo của tôi.
Dữ liệu để tinh luyện máy tính (machine learning) cần phải phức tạp và có chu kỳ. Vì một hiện tượng nào đó hoàn toàn ngẫu nhiên không chu kỳ thì không học (tiên đoán) được. Còn có chu kỳ nhưng đơn giản thì không cần phải học.

Tôi cho rằng mọi sự việc, sinh vật, kẻ cả chúng ta. Mỗi thứ, mỗi người là một con lắc cứ đung đưa mãi mãi, lúc cao lúc thấp, lúc ngừng (khi lên đến đỉnh và đổi chiều), lúc động. Tức sanh, trụ, dị, diệt. Mỗi con lắc trong chung ta không đung đưa độc lập vì chúng ta giao tiếp với thế giới chung quanh. Chúng ta bị ảnh bởi những con lắc khác, và chúng ta cũng ảnh hưởng lên sự giao động của những con lắc chung quanh ta.
Bạn hãy hình dung bạn là một con lắc giao động theo chiều ngang trước mặt bạn. Và con lắc thứ hai là của người yêu của bạn, đong đưa theo chiều ra, vô, trước mặt bạn cùng tần số với con lắc của bạn. Và khi con lắc của bạn ở điểm cao nhất, thì con lắc kia ở điểm thấp nhất. Toạ độ phối hợp của hai con lắc sẽ là một đường tròn yêu dấu hoàn hảo.

Khi quan hệ của hai bạn được mọi người biết, tức yêu không còn dấu, sự giao động con lắc hai của bạn bắt đầu bị chi phối bởi những con lắc ngoại vi. Có thể đó là những con lắc của ủng hộ, của ganh ghét, của ghen tuông và kết quả là vòng tròn yêu dấu của bạn biến thành những hình dạng không thể tiên đoán được. Nhiều khi những con lắc ngoại vi này không những tác động lên sự giao động của bạn mà có những con lắc trở thành một thành viên lắc trong hệ lắc của bạn.
Bạn có thể mở phần điều khiển (Chain Controller) và thay đổi thông số của 2 con lắc để thấy sự thay đổi.

Chuỗi các con lắc
Khi có 2 con lắc trong một hệ thống, bạn có thể miêu tả sự vận hành của chúng qua minh hoạ hoạt hình ở trên. Nhưng Khi có từ ba con lắc trở lên, miêu tả sự vận hành qua hoạt hình không thích hợp. Vì nó sẽ tạo ra sự rối rắm khó cảm nhận bằng thị giác.
Nhưng có một cách trừu tượng khác để cảm nhận sự vận hành của hệ thống từ ba con lắc trở lên. Bạn hãy hình dung con lắc kế tiếp sẽ được nói vào con lắc trước nó và dùng vi trị của con lắc trước như là toạ độ động cho toạ độ gốc của mình. Sự nối kết này sẽ tạo nên một chuỗi các con lắc.

Chuỗi của 4 con lắc, 2 con đầu tiên tạo ra vòng tròn lớn, 2 con tiếp theo tạo ra những vòng tròn nhỏ trên vòng tròn lớn

Con lắc và toạ độ cực.
Một thiên sư ngồi yên, một vật đứng yên. Cái tĩnh đó chỉ là tương đối. Vì mọi vật vẫn quay theo vòng quay của trái đất. Dựa trên khái niệm này, tôi đã cho gốc của những con lắc nối vào vòng quay của toạ độ cực (Polar coordinator). Và nó đã tạo ra sự đa dạng trong chu trình của các con lắc.

Chuỗi của 1 con lắc với toạ độ cực. Toạ cực quay 3.3 lần nhanh hơn con tần số con lắc.

Cùng chuỗi của 1 con lắc ở trên với toạ độ cực nhưng được trình bày ở dạng tích liệu (time series)

Định lý

Cho n hàm tuần hoàn f₁(t), f₂(t), ..., fₙ(t), mỗi hàm có chu kỳ hữu tỉ là T₁, T₂, ..., Tₙ, với Tᵢ ≠ 0 và Tᵢ ∈ ℚ. Khi đó, hàm tổng:

F(t) = f₁(t) + f₂(t) + ... + fₙ(t)

cũng là một hàm tuần hoàn. Tức là tồn tại một số T ≠ 0 sao cho:

F(t + T) = F(t), với mọi t ∈ ℝ.

Bước 1: Các hàm thành phần đều tuần hoàn

Với mỗi i ∈ {1, ..., n}, ta có:

fᵢ(t + Tᵢ) = fᵢ(t)

Bước 2: Xác định chu kỳ chung

Vì các Tᵢ đều là số hữu tỉ ≠ 0, tồn tại một số T là bội chung của tất cả các Tᵢ.
Ví dụ, có thể chọn:

T = LCM(T₁, T₂, ..., Tₙ)

Khi đó, với mọi i:

fᵢ(t + T) = fᵢ(t)

Bước 3: Hàm tổng cũng tuần hoàn

Vì mọi fᵢ đều lặp lại sau thời lượng T, nên:

F(t + T) = f₁(t + T) + f₂(t + T) + ... + fₙ(t + T)
         = f₁(t) + f₂(t) + ... + fₙ(t) = F(t)

Ghi chú về chiều thời gian

Nếu T là chu kỳ thì -T cũng là chu kỳ, vì:

f(t + T) = f(t) ⇒ f(t - T) = f((t - T) + T) = f(t)

Do đó, hàm tuần hoàn lặp lại theo cả hai chiều thời gian: tương lai và quá khứ.

Ví dụ văn hóa: Thiên Can – Địa Chi

Trong văn hóa phương Đông:

• Thiên Can gồm 10 đơn vị: Giáp, Ất, Bính, Đinh, Mậu, Kỷ, Canh, Tân, Nhâm, Quý (chu kỳ 10).
• Địa Chi gồm 12 đơn vị: Tý, Sửu, Dần, Mão, Thìn, Tỵ, Ngọ, Mùi, Thân, Dậu, Tuất, Hợi (chu kỳ 12).

Khi kết hợp thành các cặp Can–Chi như "Nhâm Dần", "Quý Mão", thì chu kỳ lặp lại đầy đủ là 60 năm vì LCM(10, 12) = 60.

Đây là ví dụ điển hình cho việc cộng hai chu kỳ tuần hoàn khác nhau thành một chu kỳ lớn hơn.

Lưu ý

• Chu kỳ tổng có thể nhỏ hơn T nếu các hàm có sự triệt tiêu bên trong.
• Nếu có ít nhất một Tᵢ là số vô tỉ (như √2, π), thì hàm tổng không còn tuần hoàn nữa, mà trở thành hàm gần tuần hoàn (quasiperiodic).